Over the last couple of years I have been introduced to two card games with a similar theme - co-operating to play numbered cards in an increasing sequence - but with very different approaches. Hanabi, described in this article (Part 1), is a game of deduction - it echoes classic puzzles featuring multiple logicians reasoning not only about what they know themselves, but what they can deduce about what the others know based on what they say or do. The Mind, on the other hand, is a game of group rapport and intuition, and will be discussed in Part 2 of this article.
Images retrieved from Board Game Geek
Both Hanabi and The Mind are co-operative games. The players work together, and succeed or fail, as a team rather than as individual - they are competing against the structure of the game, rather than with each other. And in both games, each player has different information, and the channels by which they can share information with each other is strictly limited by the game rules.
The game of Hanabi - an overview
The description below is an overview of Hanabi - it is not intended to provide full details of the rules, but to provide enough of an introduction to discuss the principles behind the game. A set of English-language rules are at https://www.spillehulen.dk/media/102616/hanabi-card-game-rules.pdf.
The game is played with a deck of 50 cards. There are five colours (suits). Within each suit, there are ten cards, with the values 1-5: there are three 1s, two 2s, 3s, and 4s, and one 5.
Each player has a hand of five cards (or four cards if the number of players is large).
There are also five spaces for stacks of cards, one stack for each colour. At the start of the game, these stacks are all empty - successfully building these stacks is the objective of the game. While a stack is empty, only a 1 of the corresponding colour can be played on to it. After that, only the next number in the sequence for that colour can be played on to it (e.g. if the blue stack’s top card is a 3, then only a blue 4 can be played on to it). At the end of the game, the values of the top card of each stack are totalled up to obtain a score for the game - the maximum score being 25, if the players managed to play cards to build each stack up to 5.
In addition, the players start with a pool of three fuses (lives) - one of these is lost when any player attempts to play a card on to one of the stacks if it turns out to be not permitted (i.e. if its value is not the next in the sequence for that card’s colour). And when the third fuse is lost, the game is over.
Each turn, a player may take one of the following actions:
-
Play a card: The player selects a card from their hand. If it is a card which can be played on to its colour’s stack (i.e. the value is the next in the sequence for that colour), then it is placed face-up on top of the stack. If it is not allowed, then the card is discarded, and the players lose one of their pool of fuses.
-
Discard a card: The player selects a card from their hand, discards it, and draws a new card from the deck to replace it. The risk of discarding is that it can block progress in building the stack - for example, if both blue 3s are discarded, then the blue stack can never get past 2.
So far, this sounds trivially simple - a game for 5-year-olds to practice counting.
But there is a twist. Each player can see everyone else’s hand of cards - but not their own. So how does anyone know what to play or discard? By someone choosing not to play a card, or to discard a card, but to use their turn to take the third possible action:
- Give a clue to another player: The player either selects a colour and tells the recipient of the clue which of the cards in their hand are of that colour, or selects a value and tells the recipient which cards in their hand are of that value. (In the Board Game Arena online version of the game, the game interface shows the players what clues have been provided for each card - when playing with the physical set, the players have to remember…)
If there were no limits on giving clues, then the game would again become trivial. However, every time a clue is given, it uses up a clue token. The players have only 8 of these at the start of the game, and although they recover a clue token whenever a player discards a card, they need to be judicious in how they use them.
Reasoning about knowledge: induction puzzles
It reminded me of the puzzles where logicians are wearing coloured hats and can see others' hats but not their own (and endless variations of such scenarios), and make their deductions based not only on what they can see thesmselves, but also on the actions (or lack of actions) taken by the other participants, based on what they can see and can/cannot deduce - all based on an assumption that the other participants are equally logical. These are known as induction puzzles, and there is a detailed Wikipedia page on induction puzzles of various complexities. (Some of the most sophisticated depend on the Axiom of Choice, and assumes participants each have the ability to memorise an uncountably infinite amount of information and perform computations with uncountably infinite computational complexity. They use a neat trick, but happily we don’t need to venture there.)
A simple puzzle: the blue-eyed and green-eyed islanders
Picture credit: “Island and boat in Madang Province” by kahunapulej is licensed under the Creative Commons licence CC BY-NC-SA 2.0.
A simple example is the puzzle of blue-eyed and green-eyed islanders, presented on the Wikipedia page on common knowledge, from which the below is adapted:
The situation: On an island, there are k people who have blue eyes, and the rest of the people have green eyes. At the start of the puzzle, no one on the island ever knows their own eye color. By rule, if a person on the island ever discovers they have blue eyes, that person must leave the island at dawn; anyone not making such a discovery always sleeps until after dawn. On the island, each person knows every other person’s eye color, there are no reflective surfaces, and there is no communication of eye color.
At some point, an outsider comes to the island, calls together all the people on the island, and makes the following public announcement: “At least one of you has blue eyes”. The outsider, furthermore, is known by all to be truthful, and all know that all know this, and so on. The problem: assuming all persons on the island are completely logical and that this too is common knowledge, what is the eventual outcome?
The solution: On the kth dawn after the announcement, all the blue-eyed people will leave the island.
- If
k= 1 (i.e. there is exactly one blue-eyed islander), that person will recognise that they alone have blue eyes (by seeing that all other islanders have green eyes, and having heard the announcement from the outsider that at least one islander has blue eyes) and leave at the first dawn. - If
k= 2 (i.e. there are exactly 2 blue-eyed islanders), then no-one will leave at the first dawn - each of the two blue-eyed islanders know that there is one other islander with blue eyes, and have no reason to conclude that they have blue eyes themselves. The next day, the two blue-eyed islanders, seeing only one person with blue eyes, and noting that no one left on the 1st dawn (and therefore realising thatk> 1, i.e. that there is more than one blue-eyed islander), will leave on the second dawn. - By extending this reasoning, it can be concluded that, if there are
kblue-eyed islanders, then no-one will leave for the firstk-1dawns. Then each blue-eyed islander will be realise that there are at leastkblue-eyed islanders (otherwise the blue-eyed would have already have identified themselves and left), note that that they can only seek-1blue-eyed islanders themselves, and conclude that they themselves have blue eyes. So all the blue-eyed islanders will then leave on thekth dawn.
A more complex puzzle: ten prisoners in hats, single file
Picture credit: Adapted from “Panama hats” by skinnydiver which is licensed under Creative Commons licence CC BY-SA 2.0
A more complex puzzle is presented in the Wikipedia page of induction puzzles, from which the description below is adapted.
The situation: There are 10 prisoners and 10 hats. Each prisoner is assigned a random hat, either red or blue, but the number of each colour hat is not known to the prisoners. The prisoners will be lined up single file where each can see the hats in front of him but not behind. Starting with the prisoner in the back of the line and moving forward, they must each, in turn, say only one word which must be “red” or “blue”. If the word matches their hat color they are released, if not, they are killed on the spot. A sympathetic guard warns them of this test one hour beforehand and tells them that they can formulate a plan where by following the stated rules, 9 of the 10 prisoners will definitely survive, and 1 has a 50/50 chance of survival. What is the plan to achieve the goal?
The solution: The prisoners agree the following strategy:
- The first prisoner will count the number of red hats they see in front of them, and determine its parity (i.e. whether it is even or odd). They will then say “red” if it is odd, and “blue” if it is even. The first prisoner has only a 50% chance of surviving (they have no information about their own hat, and even if they did, this strategy doesn’t take that into account) - but this will give the others the information they need.
- The second prisoner now knows, from the first prisoner’s declaration, the parity of the number of red hats on prisoners 2-10, and can observe the parity of the number of red hats on prisoners 3-10. If these are different, then the second prisoner concludes they are wearing a red hat - if equal, then the hat must be blue. So they can correctly announce the colour of their own hat.
- The third prisoner can now similarly use the information from the first and second prisoner to determine the parity of the number of red hats on prisoners 3-10, and can observe hats 4-10, to deduce the colour of their own hat. By extending this reasoning down the line, prisoners 2-10 are guaranteed to correctly announce the colour of their own hats.
A self-indulgent joke
On this theme, I can’t resist re-telling the old joke about three logicians walking into a bar. The bartender asks “Do you all want a beer?” The first replies “I don’t know.” The second also says “I don’t know”. The third is then able to say “Yes, we do.”
Reasoning in the game of Hanabi
As a player, you have the explicit information clues you have been given - a set of facts about the cards in your hand from the clues you have been given - along with the knowledge of cards which have been discarded or have been successfully played on to the stacks and which are therefore eliminated from play.
Playing on what you have seen: In some cases, you may have enough explicit information to safely play (e.g. playing a card on to the stacks, or discarding a card which is no longer needed), without needing to take into account what other players know or what they have done.
Playing on what other players have done: In other cases, the explicit information you have may not be enough alone, but combining it with your knowledge of what the other players have or have not done and some basic assumptions on how they will play (e.g. assuming that they will play on to the stacks if they can safely do so) will give you enough to work out how you play safely yourself.
This is similar to the puzzle of the blue-eyed islanders - the islanders do not need to agree a joint strategy between themselves, but knowing the rules they are all mysteriously required to follow and seeing what actually happens gives them the information they need. (The situation in Hanabi will not be quite as clear-cut as the islanders, as Hanabi players have freedom in how they play unlike the islanders mysteriously compelled to follow the strict rules, but there are still some plausible basic assumptions on how they will act.)
Playing on what others players have done, and conventions for what that will mean: Neither of those levels of reasoning is likely to get a group to a successful outcome - they won’t provide the players with enough information to make the plays they need. To improve their chances, like the 10 prisoners discussing their strategy before being lined up, players of Hanabi have built up a number of conventions - principles which state what players will do in the game in certain scenarios. With a shared set of conventions, the group can deduce more from a player’s action about what that player sees/knows than they otherwise would (assuming, of course, that the player remembered to follow the convention…) - or, conversely, a player can know how a clue or other action they take will be interpreted.
A number of common conventions and strategies have been built up - I found the Board Game Arena page Hanabi : A beginner’s guide to conventions and strategies a useful one-page introduction, and there is a detailed tutorial at The Hypen-ated Conventions - a site which I wish I’d read when I was first introduced to the game! Some conventions appear to be assumed common knowledge among players who have played a little, while the Hyphen-ated Conventions Learning Paths lists out a set of conventions and recommends that a group (particularly with newer players) agree beforehand which of them they will use when they play.
Examples of conventions: An example of a simple strategy is the Prompt_*. The example and diagram below are based on material from The Hyphen-ated Convention’s introduction to The Prompt, published under the Creative Commons licence CC BY-SA 4.0.
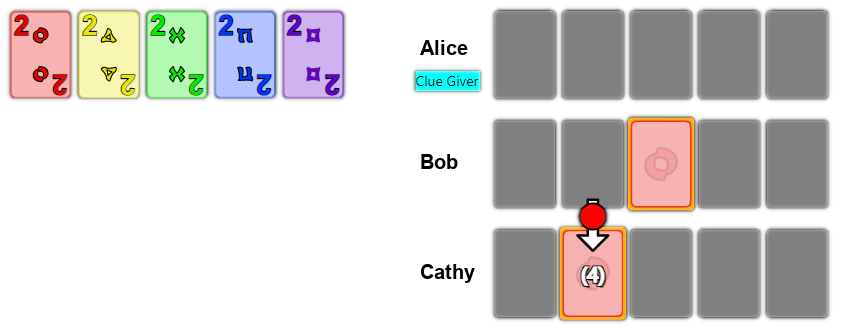
- The top card in the red stack is currently a 2.
- Bob has been given a clue identifying one card in his hand as red, but the full identity of the card is still unknown to him. In this situation, he knows by convention he is supposed to just keep the card in his hand and continue to discard unclued cards.
- Alice clues red to Cathy, which touches a red 4 (so Cathy knows this card in her hand is red, but not its value). This must be a Play Clue (i.e. a clue to Cathy that the card should be played) on the red 4.
- Bob sees that red 4 is currently unplayable, since the red 3 is not played yet. Thus, this clue implies that someone has the red 3.
- Bob does not see a red 3 clued in anyone else’s hand. So, Alice must be promising him that his unknown red card is red 3 and that he can safely play it.
The Prompt is classified in the Hyphen-ated Conventions as a fundamental convention. Other conventions building on those ideas include:
- Finesse: This can be used in a similar situation to the Prompt described above, but where Bob does not have any clued cards (and his leftmost card is the Red 3). Cathy’s clue still implies that someone has the Red 3, Bob has no indication which of his cards it is, and by convention, he plays his leftmost card with a happy outcome.
- Bluff: In the same situation as the Finesse - if Alice wants Bob to play his leftmost card - even if it isn’t the red 3 - she could clue Red to Cathy as if were a Finesse, let Bob make the deductions and follow the convention and play his leftmost card. Then Cathy needs to notice that Bob played an unclued card, deduce that Bob identified the situation as a Finesse (incorrectly, but Bob wasn’t to know…), which means that Alice’s clue to Cathy must have been for a card which was one away from playable (i.e. the Red 4). So Cathy knows she can’t play that yet.
And there are many more conventions described in the Learning Paths on how to play, discard, or clue - and conversely what other players can deduce from, and how they should respond to, such actions. So we proceed from basic prompts and finesses through 23 levels of complexity, featuring such exotically named conventions such as scream discard chop moves, gentleman’s discards, 5 colour ejections, trash bluffs, replay double ignition, and the no-information double finesse. (But I expect learning those is still easier than memorising the uncountably infinite amount of information required by some of the induction puzzles!)
Final words
So, that is an overview of Hanabi and the intricate reasoning which it can entail. In the Part 2 of this article, we will look at The Mind, where a very different type of approach to play is needed for success.
Comment on this article on Twitter:
On Hanabi, a card game of co-operative counting with scope for intricate and exotically-named strategies (gentleman's discards, trash bluffs, & replay double ignition?) - and its echoes of puzzles with logicians condemned to guess the colour of their hats: https://t.co/vmD5p7tRN9 pic.twitter.com/A39Tkw0tTa
— Terry Boon (@terryboon) August 26, 2021
Sign up to the newsletter: If you would like to be notified of new posts on this blog, please sign up to the Eclectic Stacks email newsletter.
Creative Commons licensing: This article is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.